점추정(point estimation)

 

모집단의 평균이나 분산, 비율, 상관계수 등의 모수를 추정할 때, 여러 가지 추정량을 생각할 수 있다. 예를 들어 모평균을 추정한다고 해보자. 모평균은 표본평균으로 추정할 수도 있고 표본 중위수로 추정할 수도 있으며, 표본에서 얻은 절사 평균을 사용할 수도 있다. 이때 표본평균, 표본 중위수, 표본 절자 평균 등은 모집단의 평균을 추정하기 위한 추정량(estimator) 들이다. 실제로 표본을 관측하여 이들의 값을 계산하면 그 값들은 추정 값(estimate)이 된다. 표본평균과 표본 중위수, 표본절사평균의 값들은 표본에 의지하므로, 표본에 따라 같을 수도 있지만 일반적으로는 다 다를 것이다. 그렇다면 어떤 것을 사용하여 추정하는 것이 가장 좋을까? 이 질문은 곧 어떤 추정량이 가장 좋은 추정량인가 하는 질문이 될 것이다. 상식적으로 모수의 참값에 가장 '가까운' 것을 고르면 되겠지만, 추정량은 통계량이고 통계량은 확률변수이므로 표본이 달라지면 값이 달라지기 때문에 추정량의 분포를 고려하여 추정의 기준을 세워야 한다.

 

아래 그림은 추정량의 분포를 과녁을 향해 쏜 화살의 분포에 비교한 것이다. 몇 사람의 궁수 가운데 가장 활을 잘 쏘는 사람을 골라야 할 때, 직접 활을 쏘게 하여 그 결과를 비교해 볼 수 있을 것이다. 딱 한 번만 쏘아서 가장 과녁에 가깝게 활을 쏜 사람이 가장 훌륭하다고 말하기는 어렵다. 그 시행에서 뜻밖의 행운이나 불운이 있을 수 있기 때문이다. 진짜 실력을 알려면 여러 번의 시행을 통해 전반적으로 파악하는 것이 좋다.

 

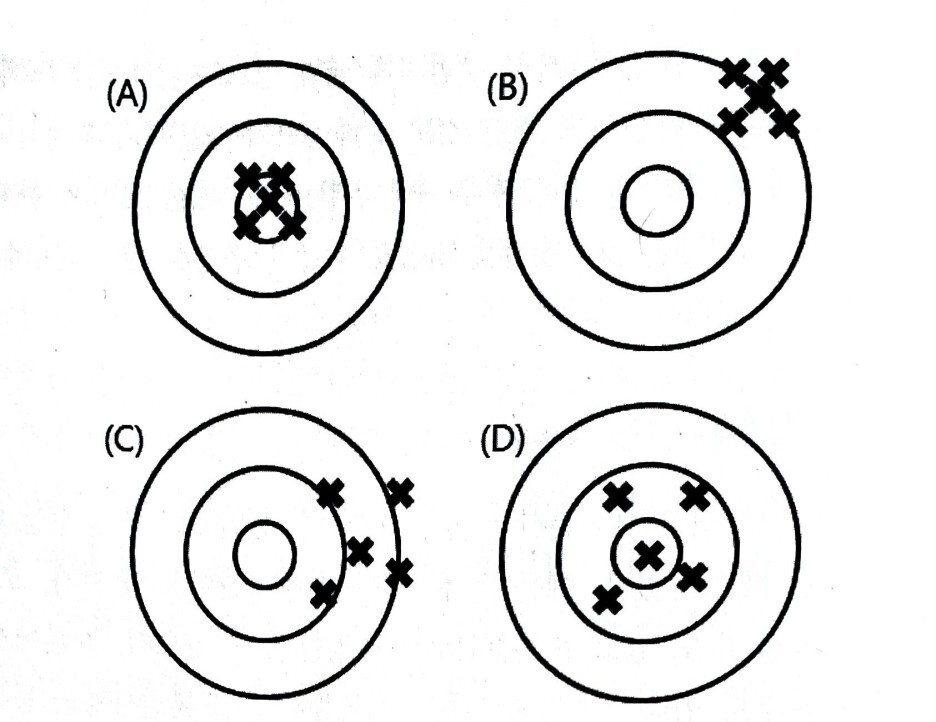
네 명의 궁수 A, B, C, D가 쏜 화살의 분포라고 한다면,

궁수 A가 가장 훌륭하다고 판정할 수 있을 것이다. 모든 화살이 고르게 과녁 한가운데를 맞췄기 때문이다. 궁수 A가 쏜 화살은 서로 매우 가까이 있고, 과녁 한가운데를 중심으로 분포하고 있다. 궁수 B가 쏜 화살은 서로 매우 가까이 있지만, 과녁 한가운데를 중심으로 하지 않고, 모두 오른쪽 위로 편향되어 있다. 궁수 C가 쏜 화살도 오른쪽으로 편향되어 있고, 이들은 서로 붙어있지 않고 넓게 퍼져 있다. 궁수 D가 쏜 화살은 넓게 퍼져 있지만 그래도 과녁 한가운데를 중심으로 퍼져 있다.

 

궁수를 추정량에, 궁수가 쏜 화살을 추정 값으로 비교하여 생각해 보자. 궁수의 실력을 화살 하나로 판정할 수 없듯이, 추정량의 좋고 나쁨을 관측 값 하나로 판단하는 것은 무리이다. 표본을 많이 뽑아서 각 표본에 대한 추정 값을 계산하여 그 값들의 분포를 보고, 즉 추정량의 분포를 통해 결정해야 하는 것이다. 추정량의 분포를 화살의 분포에 비교해 보면, 화살이 서로 매우 가까이 있는 것은 표본이 달라지더라도 추정 값은 크게 다르지 않다는 것이고, 화살이 과녁 한가운데를 중심으로 분포하고 있다는 것은 추정 값들이 모수의 참값을 중심으로 분포한다는 것이다. 첫 번째 성질은 추정량의 분산에 관한 것이고, 두 번째 성질은 추정량의 편향에 관한 것이다. 추정 값들이 가까이 있으면 추정량의 분산이 작은 것이고, 넓게 퍼져 있으면 분산이 큰 것이다. 추정 값들이 모수의 참값을 중심으로 분포하면, 즉 추정량의 기댓값이 모수의 참값과 같으면 추정량은 편향이 없는 것이고 그렇지 않으면 추정량은 편향이 있는 것이다. 좀 더 엄밀하게 말하자면, 추정량의 편향은 추정량의 기댓값에서 모수의 참값을 뺀 것으로 정의된다.

 

그림에서 보듯이, 분산도 작고 편향의 절댓값도 작은 것이 좋은 추정량이라고 할 수 있으므로 추정의 기준을 다음과 같이 평균제곱오차로 잡을 수 있다.

 

평균제곱오차(mean square error) = 분산(variance) + (편향(bias)) 2

 

다른 추정의 기준도 생각할 수 있지만, 평균제곱오차를 널리 사용하며 이 책에서도 추정량들을 비교할 때 평균제곱오차를 사용하기로 한다. 특별히, 편향이 0인 추정량은 비편향추정량(unbiased estimator)이라고 한다.