중심극한정리(central limit theorem)

 

영국의 수학자 드무아브르는 시행 횟수 n이 아주 큰 경우 이항분포가 어떤 식에 가까워질지를 연구하였고, 마침내 1733년에 발표한 논문에서 드무아브르는 문제의 식이 다음과 같이 표현됨을 증명하는 데 성공하였다.

 

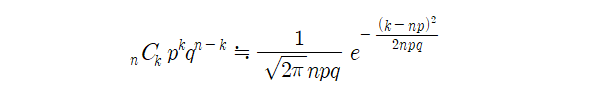
이 근사식은 시행 횟수 n이 충분히 클 때 유의미한 식이지만, 실제로는 n이 그리 크지 않아도 비교적 오차가 비교적 크지 않다. 실제 드무아브르는 “내가 시험해서 확인한 것인데, n이 100을 넘을 정도로 상당히 큰 값이 아니더라도 내 방법을 쓰면 꽤 괜찮은 결과를 얻을 수 있다"라고 기록하였다. 그는 몇 가지 경우에 대해 일일이 정확한 값을 계산하여 그 오차를 확인해 보았을 것이다. 이 근사식의 큰 의미는 이산확률분포인 이항분포에 대하여 시행 횟수 n을 충분히 크게 한다면, 연속적인 양으로 근사 시켜 연속확률분포로 해석할 수 있다는 데 있다.

 

위의 근사식에서 k의 값을 바꾸어 가며 점을 찍은 다음 매끈하게 연결하면 다음 그림과 같은 종 모양의 곡선이 된다. 이 곡선을 보면, 양쪽 끝으로 갈수록 확률이 급격하 작아지는 것을 알 수 있다.

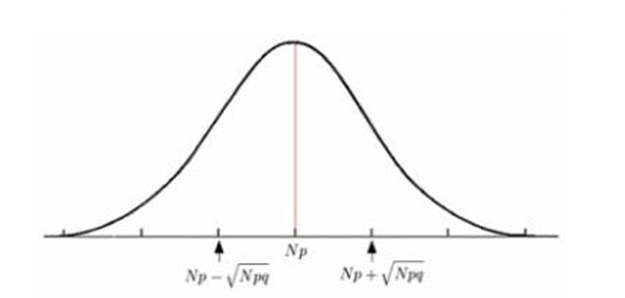
연속변수로 생각할 수 있다면 유한개의 확률을 하나하나 계산하여 더하는 대신 일정 구간에서 위의 함수를 적분하여 확률을 계산할 수 있다. 적분하면 확률이 나온다는 점에서 이런 함수를 확률밀도함수라고 한다. 이 확률밀도함수를 이용하여 나타내어지는 확률 분포를 정규분포(normal distribution)라고 한다. 이후 프랑스의 수학자 라플라스(P.-S. Laplace, 1749-1827)는 이항분포가 아닌 확률분포에 대해서도 시행 횟수가 크면 시행에 따른 평균값이 정규분포를 따름을 보였다. 이것을 중심극한정리 (central limit theorem)라 하며, 통계학의 핵심적인 이론 가운데 하나이다.